SDNE是基于深度学习处理网络嵌入问题的方法之一,另一比较重要的基于深度学习的方法是同样发表于2016年的DNGR。与DNGR相比,SDNE在利用神经网络挖掘高阶相似性的同时,利用易于捕捉的一阶相似性作为已知的监督信息。
论文的主要创新点在于将可用于降维的自编码机应用于network embedding,利用多层非线性函数捕捉网络的高度非线性结构,并利用first-order作为监督信息,并保留网络的局部结构,second-order作为无监督学习部分,保留网络的全局结构,从而整体构成一个半监督的深度学习模型。
问题概述
network embedding 的主要难点
SDNE针对以上三个难点提出了对策
- 针对网络结构非线性的问题,SDNE设计了多层非线性函数深度学习模型,将网络的非线性结构映射到高度非线性的潜在空间,更好地捕捉网络结构。
- 对于全局和局部结构保留以及稀疏性问题,SDNE结合使用网络的first-order和second-order。first-order反映网络局部结构,second-order反映网络全局结构。并且由于second-order的思想是衡量两个节点的共同临近点的相似程度,其提供的信息量远远大于first-order,所以加入second-order在一定程度上应对了网络稀疏的问题。
论文提出的主要模型如文章开头所述:
将可用于降维的自编码机应用于network embedding,利用多层非线性函数捕捉网络的高度非线性结构,并利用first-order作为监督信息,并保留网络的局部结构,second-order作为无监督学习部分,保留网络的全局结构,从而整体构成一个半监督的深度学习模型。
在针对于网络嵌入的顶点分类、连接预测、网络可视化的多个数据集的多个任务中,SDNE的表现都较为出色。
SDNE模型
模型中用到的符号含义如下表

n为网络中定点个数,K为SDNE深度模型层数,S为网络的邻接矩阵,Xi为顶点i的邻接向量,X^i为经过自编码和解码后重构的顶点i的邻接向量。Yk为自编码器第k层的输出结果,W、b是相应层的weight和bias参数。
SDNE基本架构如下图
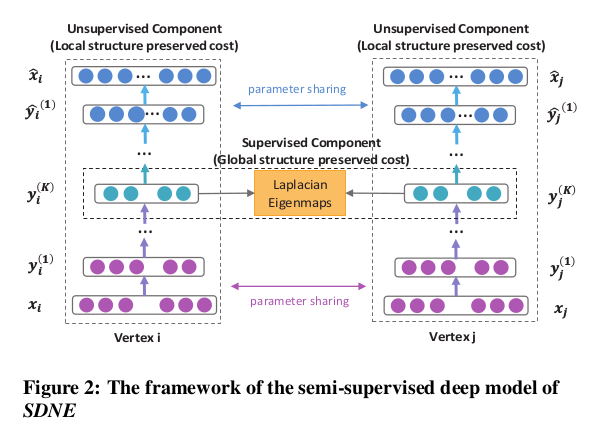
自编码器在降维过程中需要我们设定一个LOSS Function,使得自编码器以取得最小LOSS为目标学习出最佳模型。
那么重点来了,SDNE设定Loss的过程如下:
- 首先,我们希望经过编码和解码重构后的Xi与输入时相比,误差越小越好,所以Loss中的一项可以表示为:
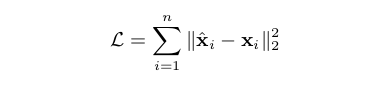
但还有一点需要注意,在顶点i的邻接向量Xi中,1值代表与相应顶点有连接,0代表与相应顶点无连接。但由于网络的稀疏性和高阶相似性等原因,Xi所代表的含义应该是:如果某值为1,则两点间一定存在相似性,如果某一值为0,也不能说明两点间无相似性。所以在重构X时,我们鼓励0值的重构。反映在Loss函数上,即为:对1值重构的惩罚重于对0值重构的惩罚。故将上式完善如下:

学过线性代数的应该都看得懂,不做过多解释。另外,在论文最后的实验部分,作者也强调beta参数不能设定的过大,因为beta越大,意味着我们越鼓励自编码器挖掘和增加无连接节点对间的联系,但两节点间first-order为0本身就反映着一定程度的不相似性,所以将beta设置地过大导致各节点对的相似性都增加是不合理的。 - 另外,我们提到SDNE中使用了first-order作为监督信息,如下式:
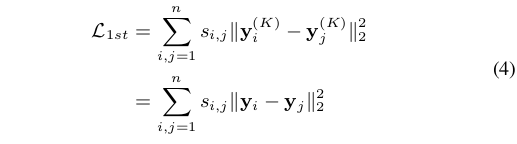
Y为自编码输出结果,上式标识的意义是,first-order为1的两点在自编码后相似性也应该比较大,两者相似性越差则Loss越大。这是SDNE作为一个半监督模型的有监督部分,同时也对应着网络的局部结构。反映在SDNE的模型图中就是中间的验证部分。 - 最后,说到Loss函数一定少不了正则化来防止过拟合,不了解这一概念的同学可以去补一下机器学习的基础。
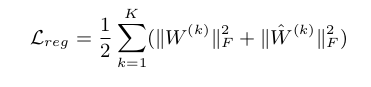
三个Loss合并如下式,就是SDNE最终的LossFunction了:
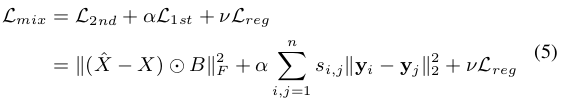
依据此收敛后的自编码器就可以作为NetworkEmbedding的降维器使用了。总结
SDNE是最早将深度学习引入网络嵌入领域的方法之一,因为应用了多层的非线性函数、结合了一阶和高阶相似、并引入了一阶相似的监督信息,有着较好保留网络的高度非线性结构、对抗稀疏性,保留局部和全局结构的有点。在本文最后的实验中,SDNE证明了它在节点分类、连接预测和网络节点可视化上的优异表现。SDNE的代码已被开源在 https://github.com/suanrong/SDNE 如果有必要,我会在之后针对SDNE的实验部分再写一篇笔记。
